TRANSLATE
ÜYELİK GİRİŞİ
MATEMATİK YORUMLARI
- MATEMATİKLE BARIŞ
- DÜRDANE ELHAN
- GÖKHAN VELİ KİŞİOĞLU
- KOLAY GELSİN DON KİŞOT!
- BASRİ KÖSELER
- EZBERLE BAŞLAYAN MATEMATİK HÜSRANLA BİTER!
- NİYETİM BAĞCIYI DÖVMEKTİ!
- BU KİTAP BENİ MATEMATİKLE BARIŞTIRDI!
- “MATEMATİKLE BARIŞIYORUM” KİTABINIZ HAYALLERİMİ GERİ VERDİ!
- KORKULU RÜYAM SONA ERDİ!
- MATEMATİKLE BARIŞIYORUM'U BİR SOLUKTA OKUDUK!
- NECİP HOCAM, BİZE ZORU ÖĞRETTİLER!
- MATEMATİĞİ SEVMEYEN BİR ÖĞRENCİYDİM!
- BEN DE MATEMATİKLE BARIŞTIM, SIRA SİZDE!
- İŞTE GAYRETİN VE ISRARIN ESERİ
- TOPLUMUMUZDA ÇIĞIR AÇACAK KİTAP!
- MATEMATİKÇİNİN MİHRİBAN TÜRKÜSÜ
- KİTABINIZ OĞLUMUN SİVİLCELERİNİ GEÇİRDİ
- Çarpım Tablosu Toplama İşlemidir
- MATEMATİKTE DEĞİŞİMLER DÜŞÜNCEYLE BAŞLAR!
- ankarali-alinin-matematikle-barismasi
- EZBERSİZ ÇARPMA
- TÜM YORUMLAR
MAKALELER
- MAKALELER
- Üstadından Makaleler-5
- Üstadından Makaleler-4
- Üstadından Makaleler-3
- Üstadından Makaleler-2
- Üstadından-makaleler-1
- egitim makaleleri
- Kitap Tanıtımları
- Öğretmenlik
- Mutlu Bir Öğretmen Olmak
- Her öğretmenin yaptığı 7 hata
- Çocuğun kalbine giden yol
- Öğretmen-Hakları
- Sınıf Yönetimi
- Eğitimcinin enstrumanı
- elbirlik bogdunuz cocuklari
- egitim-koclugu
- hız herkesin hızını keser
- egitimin-e-si
- Kanadı-Kırık-Çocuklar
- geçti borun pazarı…
- Sevgili-öğretmenim
- İki Mustafa Aşkına
- veliyi-ikna-etmek
- ogretmen-evraklari
- Etut Merkezi Belgeleri
- Matematik-sözleri
- Atatürk ve Matematik
- Matematik Nedir
- Eğitimde Teknoloji
- arduino-dersleri
- E- KİTAP
- Matematikle Barışıyorum
- Matematikle-Kucaklaşıyorum
- bolum-9- basari yolunda genclere tavsiyeler
- başarıyı engelleyen tuzaklar
- bolum-7 matematik dersinde uyguladigim ilkeler
- Matematik-başarısında-öğrencinin-rolü
- bolum-5 egitimimizin kanayan yarasi
- bolum-4 matematik basarisinda ogretmenlerin rolu
- bolum-3 matematik basarisinda ailenin rolu
- bolum-2 matematikle tanisiyorum
- bolum-1 matematikle barisiyorum
- Resimli Matematik Sözlüğü
- What is Math
- Kitap Tanıtımları
- ozlu-ozler
- Matematikle Barışıyorum
MATEMATİK DÜNYASI
- MATEMATİK TARİHİ
- Matematik-sembollerinin-kökeni
- İlginç Matematikçiler
- farklı matematik makaleleri
- MATEMATİK HİKAYELERİ
- Matematik-hikayeleri
- MATEMATİKTE NEDEN ÇUVALLIYORUZ?
- MATEMATİK ANILARI
- İlginç-mat-paylaşımları
- Ayvaz Öğretmen Gitti, Benim İçin Matematik Bitti!
- Takdirnameye Uzanan Yol
- Hocamın ellerinde geleceğim kurtuldu
- Matematik-anıları
- Matematiği Döverek Öğretmeye Çalışan Bir Öğretmenim Vardı!
- Bana Lazım Olan Soru Bankası Kitapları Değilmiş!
- Matematiğin Aydınlık Yüzü
- Matematiğin Karanlık Yüzü!
- Matematikten-kaçarken-kucağına-düştüm
- Matematik-nerelerde-karşımıza-çıkar
- Bu Dersi Bu Çocuklara Sevdirmeliydik
- ezber kabusum sona erdi
- Matematik-öcü-değil
- ezbere öğrenmişiz aslında basitmiş
- Matematik-öğretmenliğimin-ilk-dersi!
- Matematiği-sevmiyordum
- EĞİTİM MASALLARI
- Matematik-öğretiminde-çocuk-edebiyatı
- Yitik-Bir-Masal
- Umutlu Bir Masal
- melek-ana-ve-sokak-kedisi
- aslanlar-kaplanlar-ve-karıncalar
- Babamın-Minderi
- Ardında-Bir-Kitap-Bırakmalısın
- Mavi-Kelebek-ve-Balarısı
- TAŞ
- Şefkatle-sütbeyaz
- bozkir masali
- kara-cicek
- KIZIMA-MEKTUP
- ciglik
- karsinizda ayi mi oynuyor
- koca-cinar-ve-kamplumboga
PRATİK MATEMATİK
- PRATİK ÇARPIM
- PRATİK YOLLAR
- Ondalık-sayılar-pratik-kurallar
- Rasyonel-sayılar-pratik-kurallar-2
- Kesirler-pratik-yöntemler
- bolme-pratik-kurallar
- Problemler-pratik-yöntemler
- Köklü-sayılar-kısa-yollar
- Üslü-sayılar-pratik-yollar
- basamak-pratik-yollar
- Bölünebilme-pratik-kurallar
- ardisik-sayıilar-kisa-yollar
- Karmaşık-sayılar-pratik-yöntemler
- Matematik-kısa-yollar
- İSPATLAR
EĞLENCELİ MATEMATİK
- EĞLENCELİ MATEMATİK
- eglenceli-matematik
- Çarpım tablosunu doğru öğretmek
- Pozitif-ve-negatif-sayıların-çarpımı-ve-bölümü
- bir hafta neden 7 gün
- Seksek-oyunu-ve-matematik
- Pizza-ve-silindirin-hacmi
- Fincan ve hacim
- geometrik şekillerle uçurtma tasarımı
- Matematik-ve-sanatsal-şekiller
- 9-ile-carpma-etkinligi
- Plastik-tabak-daire-ve-çember
- Paskal-ve-binom
- Matematik Karikatürleri
- EĞLENCELİ MATEMATİK -B
- Kesirler-ve-kuşlar
- balonlarla-matematik
- Yılbaşı-matematik-etkinlikleri
- Sayı-mutlumu-mutsuzmu
- Daire ve balık
- Koordinat-sistemi-ile-resim-çizmek
- Çıkarma işlemi ve resim
- dondurma ve matematik
- hepimiz kareyiz
- ayak-boyu-ve-bilegimiz
- birim cember
- matematigi-yiyorum
- Lego-ile-matematik
- Parmaklarla-trigonometri
- EĞLENCELİ MATEMATİK -C
- MATEMATİK ŞARKILARI
- MATEMATİK OYUNLARI
- matematik-oyunları
- zeka-kupu-oyunu
- Matematik-ve-sihirbazlık
- Yaş-bulma-oyunu
- Yaş-ve-ev-numarası
- İlginç-matematik-örnekleri
- Kimlik-numarası-oyunu
- Aklından Bir Sayı Tut
- favori tatil noktan testi
- eglenceli koordinat sistemi
- Matematik-şakaları
- Matematik Oyunları-Video
- Tombala-ve-matematik
- Labirent-oyunu-hacim
- hangi-gun-dogdunuz
- MATEMATİK BULMACA
- MATEMATİK BİLMECE
OKUL BAŞARISI
- AYT MATEMATİK
- ÖĞRENMEYİ ÖĞRENME
- Kolay-ingilizce-nasıl-öğrenilir
- matematigi-nasıl-ogrenmeli
- Sıfırdan-matematik
- geometri nasıl çalışılır
- biyoloji ogrenme yontemleri
- Fizik Dersi Öğrenme Yöntemleri
- coğrafya nasıl öğrenilir
- kimya-ogrenme-teknikleri
- egitim-yontemlerimiz
- edebiyat-netlerini-arttirmak
- dil ve anlatim dersi ogrenme yontemleri
- calculus nasıl öğrenilir
- Sınavlara-hazırlık-taktikleri-2
- sınavlara-hazırlık-taktikleri-1
- EĞİTİMDE FARKLI BİR YÖNTEM
- Öğrenmeyi-öğrenme
- Özet-nasıl-yapılır
- Öğretim-yöntemimiz
- Felsefeyi nasıl öğrenmeli
- SIFIRLAMA YÖNTEMİ
- TEMEL MATEMATİK
- 9. Sınıf Matematik
- Köklü-sayılar
- Mutlak-değer
- Üslü-sayılar
- çarpanlara ayırma
- Problemler-nasıl-çözülür
- Günlük hayatta oran orantı
- 1.dereceden-denklemler
- Rasyonel-sayılar
- Tam-sayılar
- Obeb-okek
- bolunebilme kurallari
- Mantık-konu-anlatım
- 1.derece-eşitsizlikler
- Temel-matematik
- proje-dersi-calisma-sorulari
- kumeler-konusu
- SAYILAR
- oran-oranti
- siralama-ve-basit-esitsizlik
- GEOMETRİ
- SINAVLAR
- MÜFREDAT-KONULAR
YAŞAM VE MATEMATİK
- YAŞAM VE MATEMATİK
- Yaşam-ve-matematik
- ASTRONOMİ
- Matematik-proje-örnekleri
- hayat ve logaritma
- Fractal Geometri
- e sayısı uygulamaları
- Finans Matematiği
- Matematiksel-modelleme
- Günlük hayatta fonksiyon
- Günlük hayatta kümeler
- elips ve gunluk hayat
- bilgisayar-ve-matematik
- Matematiği-konu-alan-kitaplar
- Spor-ve-matematik
- saglik-ve-matematik
- Matematik-okuryazarlığı
- Sanat-ve-matematik
- Yaşam-ve-matematik
- DOĞADAKİ MATEMATİK
PSİKOLOJİ
- SEVGİ VE MATEMATİK
- MUTLULUK
- YARATICI KAFE
- ANNE BABA OKULU
- PSİKOLOJİ VE MAT
- KARİYER
SİTE MENÜSÜ
SİTE HARİTASI
ZİYARET BİLGİLERİ
| Aktif Ziyaretçi | 7 |
| Bugün Toplam | 413 |
| Toplam Ziyaret | 2872295 |
Matematik fotoğraf sanatında nasıl kullanılır
07/05/2022
matematik-ve-fotograf-sanati
matematikkafe.com
Diyafram ve Matematik
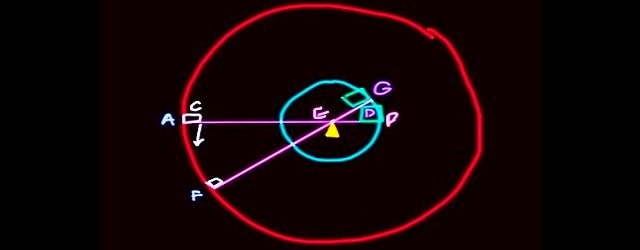
Kameralarda veya fotoğraf makinelerinde diyaframı anlamanın en iyi yolu göz bebeğimizin nasıl çalıştığını anlamaktır —göz bebeğimiz ne kadar büyürse, gözümüze o kadar fazla ışık girer.
Ortamın durumuna bağlı olarak, sensöre daha çok veya daha az ışığın düşmesini sağlamak için diyafram açıklığının çapı değiştirilir.
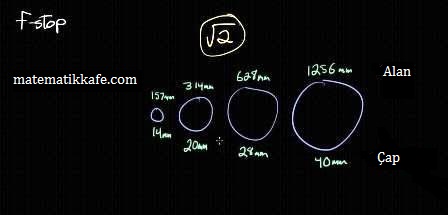
Diyafram açıklığı (apertür) f-stop veya f-durağı denen birimle ölçülür. Kamera göstergeleriniz üzerinde rakamlar görürsünüz. Buradaki rakam apertürün (ışığın içinden geçtiği açıklık) ne kadar genişlikte olduğunu gösterir. Bu değer fotoğraflarınızda özellikle 2 şeyi etkiler: Pozlama ve alan derinliği. Buradaki sayı ne kadar küçükse apertür o kadar geniştir.
Önce f-stop değerlerini yazalım:
f/1.4 – f/2 – f/2.8 – f/4 – f/5.6 – f/8 – f/11 – f/16 – f/22.

Önce f-stop değerlerini yazalım:
f/1.4 – f/2 – f/2.8 – f/4 – f/5.6 – f/8 – f/11 – f/16 – f/22.

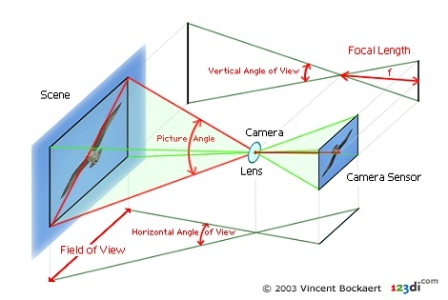
Bunlar tam duraklardır. Bu değerler hakkında bilmeniz gereken en önemli şey, birbirini takip eden her rakamda, apertür genişliği yarı yarıya azalır ve böylece lensten içeriye %50 daha az ışık girişi mümkün olur. Buradaki rakamlar rastgele gibi görünse de, apertür genişliği ile lensin odak uzaklığı arasında kullanılan bir denklemden elde edilen değerlerdir.
Günümüzde kameralar üzerinde bu listedeki değerler arasında kalan, örneğin f/3.5 gibi başka rakamlara da rastlıyoruz. Bunlar, listemizdeki tam duraklar arasında yeralan 1/3 veya 2/3 durak değerinde ara duraklardır ve daha ince ayar yapabilmenize yarar.
Konu ile ilgili geniş açıklama için tıklayınız
Etiketler: Fotoğraf sanatındaki matematik, kameralar ve matematik
Günümüzde kameralar üzerinde bu listedeki değerler arasında kalan, örneğin f/3.5 gibi başka rakamlara da rastlıyoruz. Bunlar, listemizdeki tam duraklar arasında yeralan 1/3 veya 2/3 durak değerinde ara duraklardır ve daha ince ayar yapabilmenize yarar.
Konu ile ilgili geniş açıklama için tıklayınız

Etiketler: Fotoğraf sanatındaki matematik, kameralar ve matematik
KÖŞE YAZILARI
|
|
|
| Doğan Ceylan | |
| BU EĞİTİM SİSTEMİ DÜZELMEZ | |
|
|
|
| Prof. Dr. Necati Cemaloğlu | |
| EĞİTİM VE YÖNETİMDE İNOVASYON | |
|
|
|
| Necip Güven | |
| ÇOCUKLARINIZ MATEMATİKTE ACILAR ÇEKİYOR | |
|
|
|
| İbrahim Demir | |
| EĞİTİMDE ÇÖZÜM ÖNERİLERİMİZ | |
|
|
|
| Prof. Dr. İbrahim Ortaş | |
| ÖĞRENCİLERİMİZ DERS ÇALIŞMAYI BİLİYOR MU?? | |
|
|
|
| Ramazan Bakkal | |
| EL AÇAN DEĞİL, EL AÇILAN ÜLKE OLMALIYIZ | |
|
|
|
| Musa Yıldırım | |
| MATEMATİĞİN DERİN ANLAMI-1 | |
|
|
|
| Funda Ertan | |
| BİR GARİP SIFIR | |
|
|
|
| Aysun Gençünal | |
| ÖĞRENME İLETİŞİMİ ÜZERİNE | |
|
|
|
| Murat Tekineş | |
| ÖĞRETMEK... | |
|
|
|
| Betül Arıkanlı | |
| ALMA VERME DENGESİ | |
|
|
|
| Anıl Yeşildağ | |
| HAREKET GERÇEKTEN VAR MI? | |
|
|
|
| Gülsena Öksüz | |
| ÇOCUKLARDA ÖZGÜL ÖĞRENME GÜÇLÜĞÜ | |
|
|
|
| Necmettin Türkoğlu | |
| EĞİTİMDE YAZILIMIN ÖNEMİ | |
|
|
|
| Nazire Şevval Argunşah | |
| KRİPTOLOJİ NEDİR? | |
|
|
|
| Hatice Nurseven Evren | |
| KENDİMİZDEN DÜNYAYI SEYRETMEK | |
|
|
|
| Yusuf Alkanlı | |
| 21.YÜZYILDA İKTİSAT EĞİTİMİ | |





