
Tarık Taşpınar'dan yeni teoremler
13/12/2023
yeni-teoremler
Tarık Taşpınar'ın aşağıda matematik literatürüne yeni kazandırdığı çalışmasını yayınlıyoruz. Bu çalışmayı word dosyası olarak da indirebilirsiniz. Word dosyası olarak indirmek için TIKLAYINIZ
BİR ÜÇGENDE ORTİK ÜÇGEN VE YÜKSEKLİK AYAKLARINDAN KENARLARA ÇİZİLEN DİKMELER ARASINDAKİ BAĞINTILAR
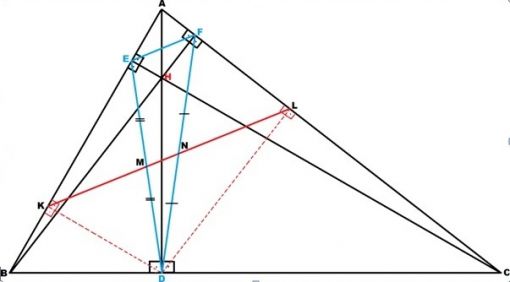
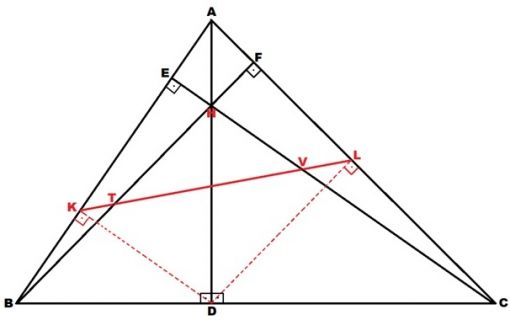
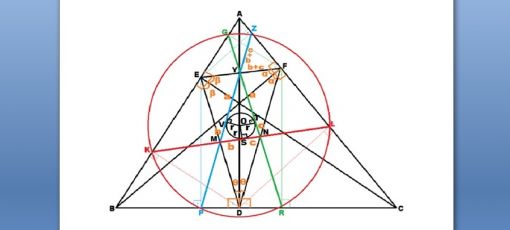
- 1) EFD üçgeni ABC üçgeninin ortik üçgeni olmak üzere, ABC üçgeninin yükseklik ayaklarının herhangi birinden (şekilde D noktası) diğer kenarlara çizilen dikmelerin (|DK| ve |DL|) bu kenarları kestiği noktaları (şekildeki K ve L noktaları) birleştiren doğru parçası (|KL|), EFD ortik üçgeninin kestiği her iki kenarını (|ED| ve |FD|) orta noktalarından keser.
|EM|= |MD|, |FN|=|ND|
- 2) ABC üçgeninin yükseklik ayaklarının herhangi birinden (şekilde D noktası) diğer kenarlara çizilen dikmelerin bu kenarları kestiği noktaları (şekildeki K ve L noktaları) birleştiren doğru parçasının (|KL|) uzunluğu EFD ortik üçgeninin çevresinin yarısına (1/2’si) eşittir.
Çevre (EFD) = 2 x |KL|
(|EF|+ |FD|+|ED|) / 2 = |KL|
KANITLAR:
1)
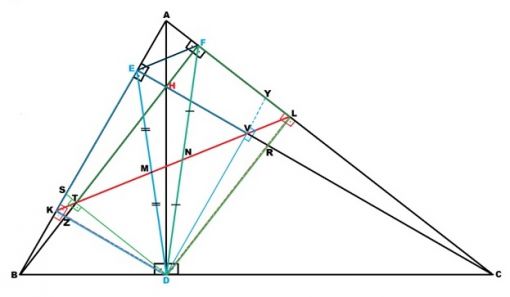
EFD ortik üçgenin |ED| kenarını inceleyelim. |KL|’nin |ED|’yi tam orta noktasından (M) kestiğinin gösterilmesi için EVDK dikdörtgenine dikkat çekmek gerekir. Şekilde de görüldüğü üzere |EC| yüksekliğine paralel ve |AB| kenarına dik olan |KD| ile |AB| kenarına paralel ve |EC| yüksekliğine dik olan |VD| doğru parçalarını çizdiğimizde EVDK dikdörtgeni oluşacaktır. (Dikdörtgen oluşması şart değildir; kare de oluşabilir.) EFD ortik üçgenine ait |ED| kenarının, EVDK dikdörtgeninin bir köşegenini oluşturduğu da fark edilecektir. |KL| nin bu dikdörtgenin içinde kalan kısmı olan |KV| doğru parçasını da dikdörtgenin |ED| ile kesişen diğer köşegeni olarak kabul edersek, |ED| ile |KL|’nin ortik üçgenin bir kenarı olan |ED|’ nin tam orta noktasında kesiştiğini de kabul edebiliriz. Zira, bir dikdörtgenin köşegenleri birbirlerini ortalar.
Ancak, |KL|’nin EVDK dikdörtgeninin köşelerinden biri olan V noktasından da geçmesi gerektiğini ayrıca göstermek gerekir. Yukarıdaki şekilde görülen AKDL ve YVRL dörtgenleri birbirine benzer ve aynı zamanda her ikisi de kirişler dörtgeni özelliği gösteren dörtgenlerdir. (Karşılıklı iki kenarları 90° ve diğer karşılıklı kenarları toplamı da 180° olduğuna dikkat edelim.) Bunlar benzerdir, çünkü şekildeki açılardan yani diklik ve paralelliklerden anlaşılacağı üzere, her iki dörtgenin kenarları diğer dörtgenin kenarlarına göre birbirine paralel ve dolayısıyla iç açıları da eşittir. Burada, YVRL dörtgeninin köşegeni olan |VL|’nin AKDL dörtgeninin köşegeni olan |KL|’nin bir parçası olduğu da dikkate alınırsa, V noktasının |EV| ile |VD|’nin kesiştiği köşede olması gerektiği anlaşılabilir. Zira, YVRL dörtgenin |YV| kenarı, EVDK’ nın |VD| kenarının aynı doğrultudaki devamıdır. Aynı şekilde, YVRL dörtgeninin |VR| kenarı da EVDK’ nın |EV| kenarının aynı doğrultudaki devamıdır. Bu bahsedilen |EV|,|VD|,|YV| ve |VR| kenarlarının kesişim noktaları V noktası olmalı ve sonuçta, |KV| de |ED| ile birlikte EVDK dik dörtgeninin köşegeni olmalıdır diyebiliriz.
Aynı şekilde, ABC üçgeninin BC kenarına ait yükseklik ayağı olan D noktasından, |FB| yüksekliğine çizilen dikme olan |TD| çizildiğinde FTDL dikdörtgeni oluşturulur ve EFD ortik üçgeninin |FD| kenarının, FTDL dikdörtgeninin bir köşegenini oluşturduğunu görürüz. |TL| de|KL|’nin bir parçası olarak yine bu dikdörtgenin diğer köşegeninin oluşturur. Yine yukarıda da açıklandığı gibi, bir dikdörtgenin köşegenleri birbirlerini ortalayacağından |KL|, |FD|’yi orta noktasından (N) keser.
Yukarıda |KL|’nin EVDK dikdörtgeninin köşelerinden biri olan V noktasından da geçmesi gerektiğinin gösterildiği şekilde ve aynı mantıkla T noktasından da geçmesi gerektiği STZK kirişler dörtgeniyle olan bağıntısı ile açıklanabilir.
Bu konuda yapmış olduğumuz inceleme ve açıklamalardan bir başka teorem-özellik de açığa çıkmaktadır:
ABC üçgeninin yükseklik ayaklarının herhangi birinden (şekilde D noktası) diğer kenarlara çizilen dikmelerin bu kenarları kestiği noktaları (şekildeki K ve L noktaları) birleştiren doğru parçası olan |KL|ile diğer kenarlara ait yükseklikler olan |FB| ve |EC|’nin kesiştiği T ve V noktalarını D noktasına birleştiren doğru parçaları olan |TD| ve |VD|, diğer yükseklikler |FB| ve |EC| ile dik açılı olur. Sonuçta, V noktası |EC|,|VD| ve |KL|’nin keşim noktasıdır. Aynı şekilde,T noktası ise |FB|, |TD| ve |KL|’nin kesişim noktası olur.
Burada belirgin olarak ortaya çıkan özellik şudur:
ABC üçgeninin yükseklik ayaklarının birinden (şekilde D noktası) diğer kenarlara çizilen dikmelerin bu kenarlarla kesiştiği noktalar ile yine aynı yükseklik ayağından (D) diğer yüksekliklere çizilen dikmelerin bu yükseklikleri kestiği noktalar ve ABC üçgenine ait ortik üçgenin o yükseklik ayağında (D) birleşen kenarlarının (şekildeki ED ve FD) orta noktalarından oluşan altı nokta (şekildeki K,T,M,N,V ve L noktaları) doğrusaldır. Ayrıca, bu noktalardan oluşan doğru, ABC üçgenine ait ortik üçgenin, bahsedilen yükseklik ayağının (D noktası) karşısındaki kenar (şekilde EF) ile paraleldir.
2)
Bu bölümde, yukarıda nitelikleri açıklanan |KL|’nin uzunluğunun, ABC üçgeninin ortik üçgeni olan EFD üçgeninin çevre uzunluğunun yarısı (1/2) kadar olduğunun kanıtları ortaya konacaktır. Bunun için öncelikle FLD dik üçgenine dikkat edilmelidir. Bu dik üçgende |NL|, hipotenüse çizilen kenarortaydır. Çünkü yukarıdaki açıklamalarımızda |KL|’nin, ortik üçgenin |FD| kenarını orta noktasından kestiği kanıtlarıyla gösterilmişti. |NL| de |KL|’nin bir parçası olduğuna göre |NL|, FLD üçgeninde |FD|’ye çizilen kenarortaydır. Bu durumda, geometri literatüründe ‘’muhteşem üçlü’’ olarak bilinen özellik gereğince, |KL|’nin |NL| kısmı, EFD ortik üçgeninin |FD| kenarının uzunluğunun yarısına eşit olacaktır.
Diğer taraftaki |ED| kenarı için ise EKD dik üçgenine dikkat çekmek gerekir. Bu üçgendeki |KM|ise hipotenüs olan|ED|’ye çizilmiş kenarortaydır. Burada da ‘’muhteşem üçlü’’ özelliğinden dolayı yine |KL|’nin bir parçası olan |KM| ise EFD ortik üçgeninin |ED| kenarının yarısına eşittir.
Buraya kadar |KL|’nin parçaları olan |NL| ve |KM|’nin uzunluklarını inceledik ve geriye |MN| uzunluğu kaldı. Burada ise M ve N noktaları EFD ortik üçgeninin iki kenarının orta noktaları olduğu için Thales Teoremi ya da temel orantı teoremi gereği |MN| uzunluğu |EF| kenarının yarısı kadar olmalıdır.
Sonuç olarak, |KL|’nin parçaları olan |KM|,|MN| ve |NL| uzunluklarının her birinin EFD ortik üçgeninin bir kenarının yarısına eşit olduğundan dolayı,
|KM|= 1/2 |ED|, |MN|= 1/2 |EF| ve |NL|=1/2 |FD|
|KL|= 1/2 (|EF|+|ED|+|FD|) eşitliklerine ulaşılır.
|KL| dışındaki ve |KL| benzeri diğer yükseklik ayaklarından diğer kenarlara çizilen dikmelerle |PZ| ve |GR| doğru parçalarının oluşturulduğu aşağıdaki şekilde ise |GR|’nin EFD ortik üçgeninin kenarlarını orta noktalarından kestiğini göstermek için GFSE ve VFRD dikdörtgenleri kullanılmıştır. Aynı şekilde |PZ|’nin orta noktalardan kestiğini göstermek için ise PFYE ve ETDZ dikdörtgenleri kullanılmıştır.
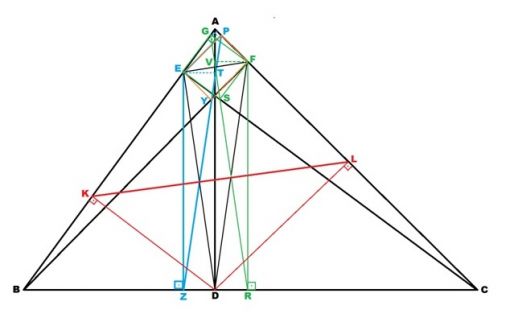
ABC üçgeninin herhangi bir kenarındaki yükseklik ayağından diğer kenarlara çizilen dikmelerin bu kenarlarla kesiştiği noktaların birleştirilmesiyle oluşan |KL|, |GR| ve |ZP| doğru parçalarının her biri EFD ortik üçgeninin çevresinin yarısına eşit olacağından, bunlar birbirine de eşittir.
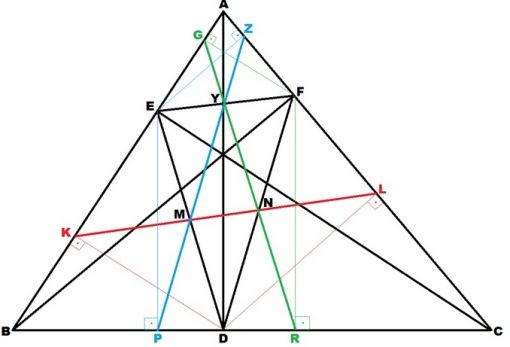
Birbirine eşit olduğunu gösterilen |KL|, |GR| ve |ZP|’yi genel olarak,
‘’Yükseklik Ayaklarından Çıkan Dikmeler Ekseni’’ olarak tanımlayabiliriz.
|KL|= |GR| =|ZP| = 1/2 (|EF|+|FD|+|ED|)
|YM| = 1/2 |FD| |EM|=|YN| |YN|=|MD|
|YN| = 1/2 |ED| |YM|=|FN| |YM|=|ND|
Ayrıca şu eşitlikler de çıkarılabilir:
|KL|= |GR| =|ZP| =|YF|+|FN|+|YN|
|KL|= |GR| =|ZP| =|EY|+|EM|+|YM|
|KL|= |GR| =|ZP| =|YM|+|YN|+|MN|
|KL|= |GR| =|ZP| =|MN|+|MD|+|ND|
EYM, YFN, YMN ve MND üçgenleri EFD ortik üçgeninin benzerleridir ve benzerlik oranları ise 1 / 2 dir. Çünkü |KL|,|GR| ve |ZP|doğru parçaları, EFD üçgenini iki kenarının orta noktalarından kestiği için YMN üçgeni bir ortalar (medial) üçgenidir. Ortalar üçgeninin özelliğinden dolayı YMN üçgeni dışında kalan EYM, YFN ile MND üçgenleri YMN ile eş üçgenler ve EFD ortik üçgeni ile benzer üçgenler olurlar.
Teorem: Bir ABC üçgeninde, yükseklik ayaklarının birinden diğer kenarlara çizilen dikmelerin bu kenarlarla kesiştiği noktaları (şekildeki K ve L noktaları) birleştiren doğru parçası ve bunun diğer kenarlara ait yüksekliklerle kesiştiği noktalar (şekildeki T ve V noktaları) arasındaki |KT|, |TV| ve |VL| uzunlukları ile LKD ve KLD açıları biliniyorsa, ABC üçgeninin ortik üçgenine ait tüm kenar uzunlukları ve açıları bulunabilir.
|KT|+|TV|=|KV|
|KV|=|ED|
|VL|+|TV|=|TL|
|TL|=|FD|
Kanıt:
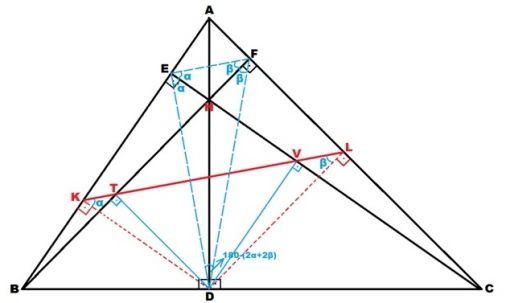
|KV|=|ED| eşitliğinin ispatı için EVDK dikdörtgenine (kare de olabilirdi) ve bunun |ED| ve |KV| köşegenlerine dikkat etmemiz gerekir. Dikdörtgende köşegenler birbirine eşit uzunlukta olacağı için |KV|=|ED| eşitliği ortaya çıkar.
|TL|=|FD| eşitliği için ise FLDT dikdörtgenine dikkat edersek |FD| ve |TL| köşegenlerinin eşitliğinden bu sonuca ulaşabiliriz.
Ortik üçgenin |EF| kenarı ise |KT|+|VL| toplamına eşit olmalıdır.
Şöyle ki;
Daha önceki konularda şekildeki |KL|’nin, ortik üçgenin çevre uzunluğunun yarısına eşit olduğunun kanıtları gösterilmişti.
2|KL|= |EF|+|FD|+|ED| eşitliğinden,
2|KT|+ 2|TV|+ 2|VL|= |EF|+|FD|+|ED|
|ED| kenarı birer |KT| ve |TV| uzunluğu içerir. |FD| kenarı ise birer |TV| ve |VL| uzunluğu içerir. Bu durumda, hemen yukarıda bahsedilen 2|KT|+ 2|TV|+ 2|VL| toplamından 2 adet |TV| ile birer |KT| ve |VL| çıkarıldığında geriye |KT|+|VL| kalır ve bu da ortik üçgenin |EF|kenarına karşılık gelir.
Ayrıca |EF| ile |KL| birbirine paraleldir. Çünkü, KLD üçgeninin |DL| kenarı |BF| yüksekliğine; |KD| kenarı ise |EC| yüksekliğine paraleldir. EFH üçgeni ile KLD üçgeni bu paralellikten dolayı benzer üçgenlerdir. Bu benzerlikten de α ve β açılarının eşitliğini çıkarabiliriz. Ortik üçgenin köşelerinde yüksekliklerin oluşturduğu açıların birbirine eşit olma özelliğinden, E köşesindeki açılar α ve F köşesinde oluşan açılar ise β açısıdır. EFD ortik üçgeninin üçüncü açısı ise 180-(2α+2β) olmalıdır.
Teorem:
ha.hb.hc = Çevre (EDF) . Alan (ABC)
Ortik üçgen ile ilgili olarak yukarıdaki eşitlik bazı kaynaklarda ispatlarıyla birlikte açıklanmaktadır. Bilinen bu eşitlikten yararlanarak ve yukarıda açıklanan konularda bahsedilen Ç (EDF) = 2.|KL| eşitliğini de kullanarak, diğer bazı eşitlik ve sonuçlara ulaşılabilir.
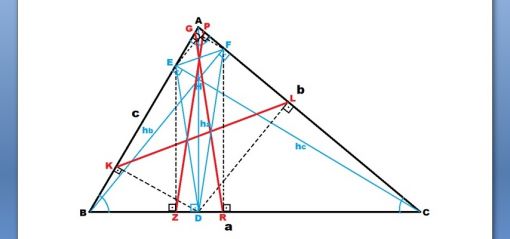


TAYLOR ÇEMBERİNE FARKLI AÇIKLAMA
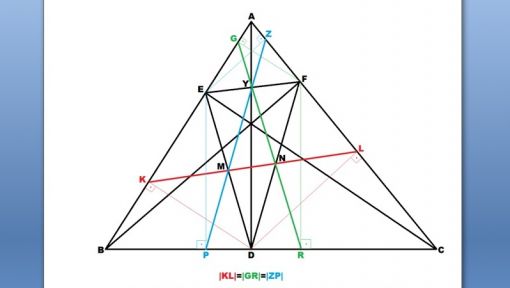
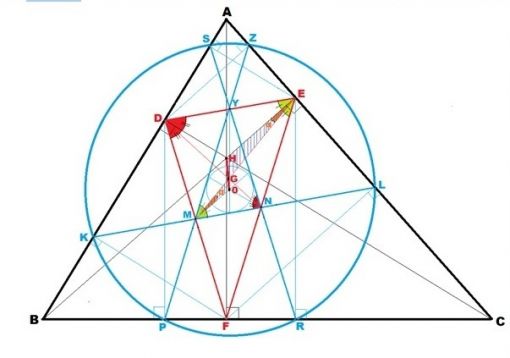
Yukarıdaki şekilde görülen, daha önceki konularda özellikleri ve birbirine eşit oldukları açıklanan,|KL|, |GR| ve |ZP| doğru parçalarının uç noktaları olan altı noktayı ifade eden K, L,G,R,Z ve P noktaları aynı çember üzerinde bulunur ve aslında bu, Taylor Çemberi adıyla bilinen çemberdir. Ayrıca bu çember, geometride Conway Çemberi olarak bilinen çemberin özelliklerini gösterir. YMN üçgeni bu Conway çemberinin çizildiği temel üçgendir.
Bir üçgende yükseklik ayaklarından üçgenin kenarlarına çizilen altı dikme ayağı aynı çemberin üzerindedir. Bu çembere Taylor Çemberi denir.
(Düzlem geometride, Conway çember teoremi, bir üçgenin her bir köşesinde kesişen kenarlar, karşı kenarın uzunluğu kadar uzatıldığında, ortaya çıkan üç çizgi parçasının altı uç noktasının merkezinin, üçgenin iç teğet çemberinin merkezi olduğunu ifade eder. Bu altı noktanın bulunduğu çembere, üçgenin Conway çemberi denir. Kaynak: Wikipedia)
KANIT:
|KL|, |GR| ve |ZP| doğru parçalarının birbirlerini tam orta noktalarından kestiklerini düşünelim. Hepsi birbirine eşit olduğu için, |KL|, |GR| ve |ZP| den her birinin çap olduğu bir çember oluşturur.
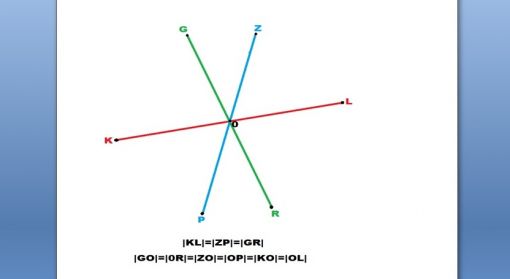
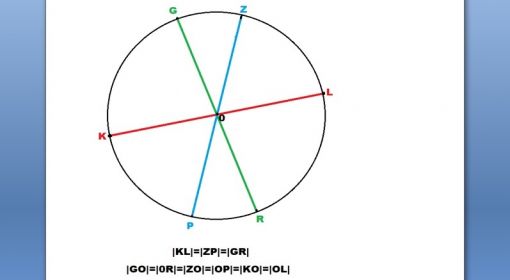
Yukarıdaki şekillerde görülen |KL|, |ZP| ve |GR| doğru parçaları, 0 merkez noktasından, önceki konumlarına paralel olarak ve aralarındaki açılar korunarak, orta noktalarından ‘’eşit miktarda’’ aşağıdaki şekilde görüldüğü gibi kaydırıldığını düşünelim.
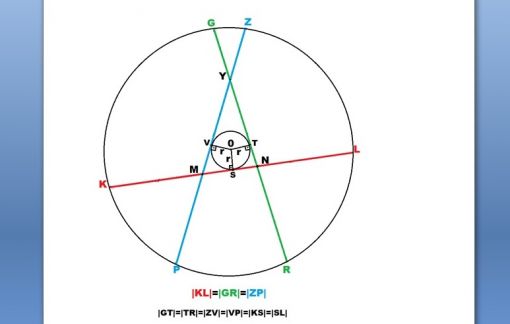
0 merkez noktasından eşit uzaklıklarda önceki konumlarına paralel olarak uzaklaştırılmasından bahsediliyorsa,|KL|, |ZP| ve |GR| nin kesişim noktaları olan Y,M ve N noktalarının köşelerini oluşturduğu YMN üçgeninin iç teğet çember merkezi olan 0 noktasına göre eşit olan uzaklıkları yani r yarıçaplarını düşünmek gerekir. Aynı zamanda bu r mesafeleri; bu kirişlerin orta noktaları olan V,T ve S noktalarına göre uzaklık olmalıdır. Bu şekilde bir kaydırma olduğunda, bahsedilen kirişlerin uç noktaları olan K,L,G,R,Z ve P noktaları birbirlerine göre yine aynı açılarda ve de aynı mesafede uzaklaşarak konumlanacağından, önceki çemberden daha büyük çapa sahip yeni bir çemberin üzerinde olmalıdırlar.
Ancak 0 merkez noktasından eşit olarak uzaklaştırılmaları, tam olarak orta noktalarından olan uzaklıkların eşitliği gereklidir. Bunların ‘’orta noktalardan eşit uzaklığının’’ ispatı için aşağıdaki şekil ve açıklamalar izah edici olacaktır:
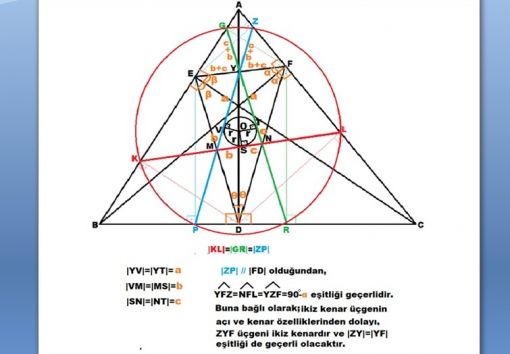

EFD ortik üçgeninin ortalar (medial) üçgeni YMN üçgenidir. Yukarıdaki konularda açıklandığı üzere, |ZP|, |GR| ve |KL|, ortik üçgenin kenarlarını orta noktalarından kestiği için bunların parçaları olan |YM|, |YN| ve |MN| bu ortalar (medial) üçgeninin kenarlarını oluşturmaktadır. Bu özelliklerden de |ZP|nin |FD| ile paralel olduğunu çıkarabiliriz. Ayrıca bu paralellikten dolayı, YFMN dörtgeninin bir paralelkenar olduğunu ve buna bağlı olarak da |YF|=|MN| eşitliğine ve dolayısıyla |ZY|=|YF|=|MN| eşitliğine de ulaşabiliriz.
|ZP|,|GR| ve |KL| nin EFD ortik üçgenin çevresinin yarısına eşit olduğunu daha önceki konularda belirtmiştik. Aynı zamanda, ortalar üçgeninin özelliklerinden dolayı, EFD ortik üçgeninin ortalar (medial) üçgeni olan YMN nin çevresi de EFD üçgeninin çevresinin yarısına eşit olur. Ortalar üçgeninin bilinen özelliklerinden dolayı, YMN nin iç teğet çemberine|YM|, |MN| ve |YN|’nin teğet olduğu noktalar bu kenarları yukarıdaki şekilde görüldüğü gibi a,b ve c bölümlerine ayırır. Bu bölümlerden oluşan 2a+2b+2c toplamının YMN ortalar üçgeninin çevre uzunluğunu ifade ettiğini görürüz. Bu durumda |ZP| nin orta noktasını araştırdığımızda, |ZV|ve|VP| nin |ZP|’nin yarısına eşit olduğu ve V noktasının ise orta noktası olduğu sonucuna ulaşmalıyız. Çünkü,hemen yukarıda bahsedilen |ZY|= |YF|=|MN| eşitliğine dayanarak; YFMN paralelkenarından dolayı|MN|= b+c eşitliği ile |ZY|= b+c eşitliğini de belirleye biliriz. |ZP|’nin yarısına eşit olduğunu belirttiğimiz |ZV|’nin uzunluğu |YV|+|ZY| toplamına eşittir. |YV|=a ve |ZY|=b+c olduğu için toplamları a+b+c olduğu sonucuna ulaştığımız için de tamamı 2a+2b+2c olduğu bilgisine dayanarak, ‘V noktası |ZP| nin orta noktasıdır’ deriz.
|EF|’nin |KL|ile; |GR|’nin de |ED|ile paralelliklerinden dolayı,aynı mantıkla S noktası |KL|’nin; T noktası ise |GR|’ nin orta noktasıdır’ diyebiliriz.
Ayrıca, YMN üçgeninin iç teğet çemberinin merkezi olan 0 noktası, aynı zamanda, K,L,G,R,Z ve P noktalarını içeren çemberin de merkez noktası olacaktır.
Ayrıca YMN üçgeni temel alınarak oluşturulan Conway çemberi özelliklerinden dolayı,
YM = NL =NR
MN = GY = ZY
YN = KM = MP
Eşitlikleri de geçerli olacaktır. Bunların yanında, EYNM ve YFNM paralelkenarlarından ve KL, GR ve ZP nin EFD ortik üçgeninin kenarlarını orta noktalarından kestiğinden dolayı yukarıdaki eşitliklere şu şekilde eklemeler yapılabilir:
YM = NL =NR = FN = ND
MN = GY = ZY = EY = YF
YN = KM = MP = EM = MD
TEOREM:

KANIT:

TEOREM:
Yukarıdaki şekilden çıkarılacak diğer bir sonuç da şudur:
Bir ABC üçgenine ait ortik üçgenin (DEF üçgeninin) ortalar (medial) üçgeniyle (YMN üçgeni) oluşturulan bir Conway çemberini belirleyen altı nokta (S, Z, L, R, P ve K noktalar), aynı zamanda o ABC üçgeninin kenarları üzerinde bulunur.
ORTİK ÜÇGENİN KENAR ORTA DİKMELERİNİN DOKUZ NOKTA ÇEMBERİ İLE İLİŞKİSİ
TEOREM:
Herhangi bir ABC üçgenine ait DEF ortik üçgeninin bir kenarına çizilen (şekilde EF kenarı)‘’kenar orta dikme’’, ortik üçgenin o kenarının (EF) karşısında bulunan ve kesişmediği kenarı (şekildeki AB) orta noktasından (K noktası) kestiği gibi; söz konusu (AB) kenarına çizilen yüksekliğin (şekildeki DC),diklik merkezi olan H noktası ile yüksekliğin çizildiği köşe olan C köşesi arasındaki (HC) kısmını da orta noktasından (L noktası) keser. Ayrıca bu bahsedilen orta noktalar olan K ve L noktaları ABC üçgeninin dokuz nokta çemberinin (şekildeki 0 merkezli çember) üzerinde bulunacağından ve ortik üçgenin kenarlarına çizilen orta dikmelerin kesişim noktası bu çemberin merkezi olacağı için (yani tüm orta dikmelerin bu çemberin merkezinden geçmesi gerektiğinden), KL doğru parçası ABC üçgenin dokuz nokta çemberinin çapını oluşturur.
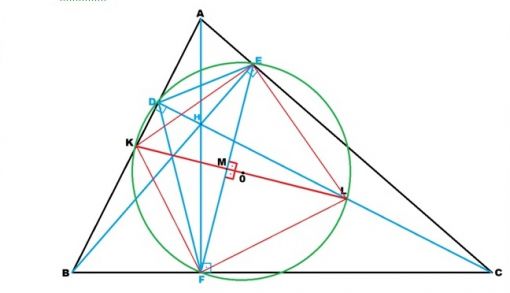
|AK| = |KB|, |HL| = |LC|, |EM| = |MF|
Kanıt:
Kanıtlar için öncelikle EHC dik üçgenine dikkat çekelim. HC kenarı hipotenüsü oluşturur. Şimdi de E dik köşesinden hipotenüs olan HC nin orta noktası olan L noktasına EL doğru parçasını çizelim. EHC dik üçgen olduğundan, geometride muhteşem üçlü olarak bilinen özellikten dolayı |EL| de |HC| nin yarısına yani |HL| ye eşit olur. Bu aşamada aynı |HC| hipotenüsünü paylaşan HFC dik üçgeninde dikkat edilirse, dik köşe olan F den HC hipotenüsünün ortası olan L noktasına |FL| yi çizdiğimizde bu da |HL| ye eşit olacaktır.
|EL| = |HL| ve |FL| = |HL| olduğundan |EL| = |FL|
Bu durumda EFL üçgeni bir ikiz kenar üçgen olacaktır. İkizkenar üçgende eşit olan kenarların birleştiği köşeden (L noktasından) karşı kenara (EF) dikme indirildiğinde o kenarı orta noktasından (M noktası) keser.
|EM| = |MF| olur. Yani bu dikme aynı zamanda DEF ortik üçgeninin EF kenarının orta dikmesi olur.
Buraya kadar anlatılanlardan, |ML|’nin, DEF ortik üçgenine ait EF kenarına çizilen orta dikme olduğu ve |HC|’nin orta noktası olan ve bu nedenle ABC üçgeninin dokuz nokta çemberinin geçtiği L’den geçtiği ortaya konmuş oldu.
Şimdi de AEB dik üçgenine dikkat edelim. Burada AB kenarı hipotenüstür. E dik köşesinden bu hipotenüsün orta noktası olan K noktasına EK doğru parçasını çizelim. Bu |EK|, dik üçgenlerdeki muhteşem üçlü özelliğinden dolayı |AB|’nin yarısı kadar olan |AK|’ya eşit olacaktır.
ABF dik üçgenine dikkat ettiğimizde, yine AB kenarının orta noktası olan K noktasına F dik köşesinden KF doğru parçasını çizersek dik üçgendeki muhteşem üçlü özelliği gereği |KF|, |AK|’ ya eşit olacaktır.
|EK| = |AK| ve |KF| = |AK| olduğundan |EK| = |KF| olur.
Bu durumda ise EKF üçgeni bir ikizkenar üçgen olacaktır. İkizkenar üçgende eşit olan kenarların birleştiği köşeden (K noktasından) karşı kenara (EF) dikme indirildiğinde o kenarı orta noktasından (M noktası) keser ve yine |EM| = |MF| sonucuna ulaşılır.
Bu anlatılanlardan, |KM|’nin de |ML| gibi, DEF ortik üçgeninin EF kenarına çizilen orta dikme olduğu ve ABC üçgenine ait AB kenarının orta noktası olan ve bu nedenle ABC üçgeninin dokuz nokta çemberinin geçtiği K’den geçtiği ortaya konmuş olacaktır.
KL ve ML nin her ikisi de EF nin orta dikmesi olduğundan, bunların birleşimi olan KL, DEF ortik üçgeninin EF kenarının orta dikmesi olacaktır. ABC üçgeninin dokuz nokta çemberi yükseklik ayaklarından geçeceği için, köşelerini bu yükseklik ayaklarının oluşturduğu DEF ortik üçgeninin çevrel çemberini oluşturur. Bir üçgenin çevrel çember merkezi o üçgenin kenar orta dikmelerinin kesişim noktası olduğu için bahsettiğimiz |KL| dikmesi de dokuz nokta çemberinin merkezinden geçmelidir. Bu durumda |KL| ABC üçgeninin dokuz nokta çember merkezi olan 0 noktasından geçtiği için ve iki ucu olan K ve L noktaları bu çemberin üzerinde olduğundan, |KL|’nin ABC üçgeninin dokuz nokta çemberinin çapını oluşturduğu sonucuna ulaşabiliriz.
Yukarıda anlatılan bilgi ve özellikleri diğer bir şekilde ifade edersek;
bir ABC üçgeninde şu noktalar doğrusaldır:
- ABC üçgenin herhangi bir kenarının orta noktası,
- ABC üçgenine ait ortik üçgeninin, orta noktası belirlenen kenarın karşısında bulunan ve bu kenarı kesmeyen kenarının orta noktası,
- ABC üçgeninin dokuz nokta çember merkezi,
- ABC üçgeninin orta noktası belirlenen kenarına ait yüksekliğin diklik merkezinden çıktığı köşeye kadar olan kısmının orta noktası.
Sonuçta yukarıdaki şekilde de görülen,
K,M,0 ve L noktaları doğrusaldır.
Buraya kadar anlatılanlar dar açılı üçgenler içindi. Geniş açılı üçgenlerde ise aralarında geniş açı bulunan kenarların uzantılarına çizilen yüksekliklerin kesişme noktası yani diklik merkezi (aşağıdaki şekilde H noktası) esas alınacaktır. K noktası, diklik merkezi H’den, yüksekliğin çıktığı köşe olan B noktasına kadar olan uzaklığın yani |HB|’nin orta noktasıdır. L noktası ise AC kenarının orta noktasıdır. Sonuçta yine DEF ortik üçgeninin EF kenarına çizilen kenar orta dikme K, L ve 0 noktalarından geçecek ve yine K, M, 0 ve L noktaları doğrusal olacak ve de |KL|, 0 merkezli dokuz nokta çemberinin çapını oluşturacaktır.
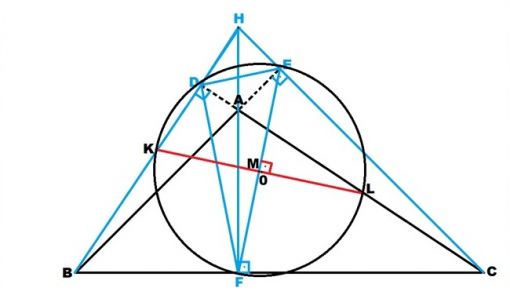
|HK| = |KB| |AL| = |LC| |EM| = |MF|
KENARLARI KESİŞEN İKİÜÇGENİN KÖŞE NOKTALARINDAN OLUŞTURULAN ALTIGENİN ALANI
TEOREM:
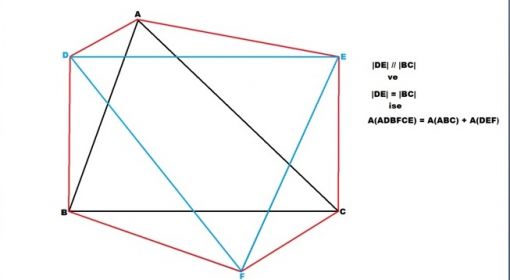
ABC üçgeni ile DEF üçgeni şekilde görüldüğü gibi bir araya getirildiğinde ve üçgenlerin köşeleri birleştirilip ADBFCE altıgeni oluşturulduğunda, bu altıgenin alanı ABC ve DEF üçgenlerinin alanlarının toplamına eşit olur.
Bu eşitliğin sağlanabilmesi için;
1-İki üçgenin en az bir kenarlarının eşit uzunlukta ve birbirlerine paralel olmalıdır. (Şekildeki DE ve BC kenarları)
2- Her bir üçgenin birbirine eşit ve paralel olduğunu belirttiğimiz kenarlarının karşısında bulunan köşeleri (şekildeki A ve F köşeleri), diğer üçgenin eşit ve paralel olan kenarının diğer tarafında olmalıdır. Şekildeki A köşesi, DE kenarının diğer tarafında ve diğer üçgen olan DEF üçgeninin sınırları içinde değildir. Aynı durum F köşesi ve ABC üçgeninin BC kenarı için de geçerlidir.
Kanıt:
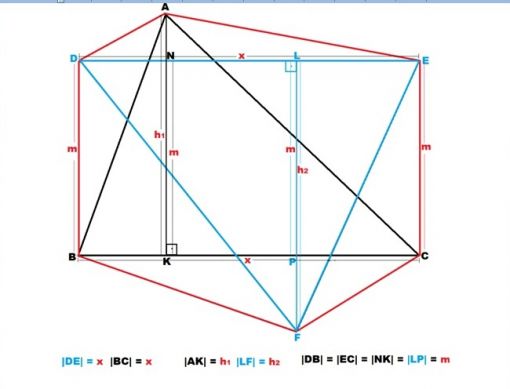
Kanıt:
ADBFCE altıgenini üç kısma ayırabiliriz:
1-ADE üçgeni
2-DECB dikdörtgeni
3-BCF üçgeni
ADE üçgeninin alanını yukarıda verilen çizim ve bilgiler ışığında formüle edersek;
ADE üçgeninin DE kenarına ait yüksekliği olan |AN|’nin uzunluğunu (h1– m) olarak kabul edildiğinde ADE üçgeninin alanı;
A(ADE) = x. (h1– m) / 2 olur.
DECB dikdörtgeninin alanını formüle ettiğimizde,
A (DECB) = x.m
BCF üçgeninin alanı ise,
BFC üçgeninin BC kenarına ait yüksekliği olan |PF|’nin uzunluğunu (h2– m) olarak kabul edildiğinde BFC üçgeninin alanı;
A(BFC) = x. (h2– m) / 2 olur.
Şimdi de ABC ve DEF üçgenlerinin alanlarının toplamı ile yukarıdaki çıkarımlardan ortaya koyulabilecek olan ADBFCE altıgeninin alanının eşitliğini formüle edersek;
A(ABC)=(x.h1) / 2 A(DEF)= (x.h2) / 2
A(ADBFCE)=[x. (h1– m) / 2 ] + [x. (h2– m) / 2]+ (x.m)
(x.h1) / 2 + (x.h2) / 2 = [x. (h1– m) / 2 ] + [x. (h2– m) / 2]+ (x.m)
(x.h1) / 2 + (x.h2) / 2 = [(x.h1) – (x.m)] /2 + [(x.h2)–(x.m) /2] + (x.m)
Eşitliğin sağ tarafındaki (x.m) nin paydasını 1 kabul edip paydaları eşitlersek;
(x.h1) / 2 + (x.h2) / 2 = [(x.h1) – (x.m)] /2 + [(x.h2)–(x.m) /2] + [2 (x.m)/2]
şeklini alır. Eşitliğin sağ tarafındaki 2 adet – (x.m) ile + 2(x.m) birbirini nötrleyip ifadeyi sadeleştirirse sağ tarafta da,
(x.h1) / 2 + (x.h2) / 2 ifadesi kalacak ve sonuçta eşitliğin iki tarafı,
(x.h1) / 2 + (x.h2) / 2 = (x.h1) / 2 + (x.h2) / 2
şeklinde eşitlenecektir. Bu eşitlik, ABC ve DEF üçgenlerinin alanlarının toplamı ile ADBFCE altıgeninin alanının eşitliğini kanıtlamış olur.
Ayrıca belirtmek gerekir ki; DE ve BC kenarlarının mutlaka dikdörtgen oluşturacak şekilde kenarlarının (aşağıda bulunan şekildeki DB ve EC kenarları) bir birini dik açıyla kesmeleri gerekmez. Dik açı dışında herhangi bir açıyla kesip paralelkenar oluşturabilirler. Bu durumda paralelkenarın alanı da taban x yükseklik olduğu için yukarıda altıgenin alanı için verilen formülde hiçbir değişiklik olmayacaktır. Sonuçta DECB, dikdörtgen de oluşturabilir, paralelkenar da...
TEOREM:
Yukarıda açıklanan teorem yardımıyla aşağıdaki şekilde açıklanan eşitliğin doğruluğunu da gösterebiliriz.
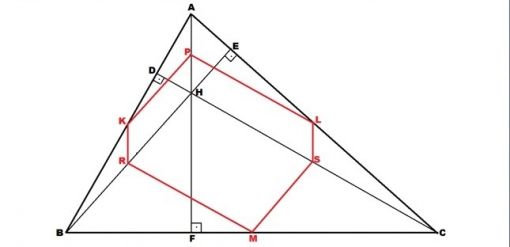

Yukarıdaki şekilde belirtilen P,L,S,M,R,K noktaları dokuz nokta çemberini belirleyen noktalardan altısıdır.
K noktası ABC üçgeninin AB kenarının; M noktası BC kenarının; L ise AC kenarının orta noktasıdır.
P noktası ABC üçgeninin diklik merkezi (H) ile A köşesi arasındaki mesafenin orta noktası, R noktası H ile B köşesi arasının orta noktası, S ise H ile C köşesi arasının orta noktasıdır.
Görüldüğü üzere, şekildeki P,L,S,M,R,K noktalarını birleştirdiğimizde bir altıgen oluşmaktadır.
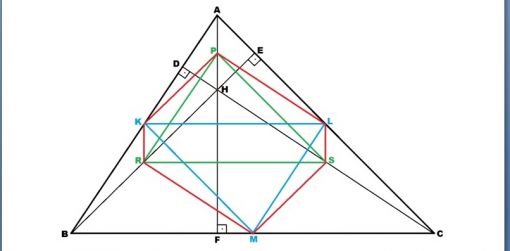
Bu altıgeni oluşturan noktalar, KLM ve PRS üçgenlerinin köşelerini oluşturan noktalardır. Yukarıda bir önceki teoremde bahsedilen özellikler bu iki üçgen için de geçerlidir. KL ve RS kenarları birbirine paralel ve eşit uzunluktadır. Daha doğrusu bu KLM ve PRS üçgenleri eş üçgenlerdir.
AHB üçgeninde PR den, AHC üçgeninde PS den ve HBC üçgeninde ise RS den yararlanarak temel orantı teoremi ile PRnin AB kenarının; PS nin AC kenarının, RS nin ise BC kenarının yarısına eşit ve paralel olduğunu gösterebiliriz. Çünkü, R nin HB nin orta noktası, P’nin AH nin orta noktası, S nin ise HC’ nin orta noktası olduğu belirtilmişti. Sonuçta, PRS üçgeni, ABC üçgeninin 1/2 oranında benzeri olur.
KLM üçgeni ise, köşeleri olan K,L ve M noktaları ABC üçgeninin kenarlarının orta nokta noktaları olduğu için ABC üçgeninin medial (ortalar) üçgenidir. Medial (ortalar) üçgeni olduğu için zaten KLM üçgeni ABC üçgeninin 1/2 oranında benzeridir.
Sonuç olarak, KLM ve PRS üçgenleri ABC üçgenine 1/2 oranında benzer ve eş üçgenlerdir.
Yukarıda açıklanan bir önceki teoremde, en az bir kenarları birbirine paralel ve (bu paralel olan kenarları) birbirine eşit olan iki üçgenin, şekildeki gibi köşelerinin birleşiminden oluşan altıgenin alanı, her iki üçgenin alanlarının toplamına eşit olduğu gösterilmişti. Burada, KLM ve PRS üçgenleri eş üçgenler ve ABC üçgenine 1/2 oranında benzerdirler. Benzer olan üçgenlerin alanlarının birbirine oranı, benzerlik oranının karesine eşit olduğu için KLM ve PRS’ nin her birinin alanının ABC üçgenine göre, 1/2’nin karesi olan 1/4’ü oranında olacaktır. Her biri ABC nin1/4’ü oranında alana sahip olduğu için toplamda ABC nin 1/4 x 2 =1/2 oranında alana sahip olacaklardır. Yukarıda bahsedilen teorem gereği de PLSMRK altıgeninin alanı ABC üçgeninin alanının yarısı (1/2’si) kadar olacaktır.
TEOREM:
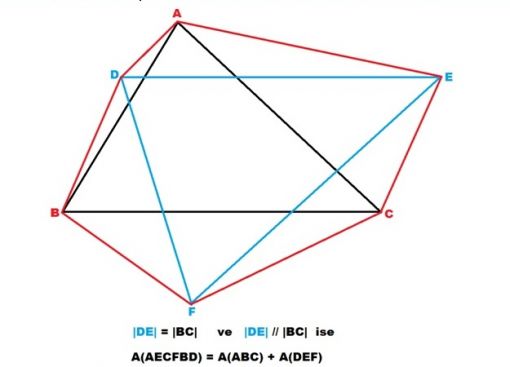
Aşağıdaki şekilde görüldüğü gibi, ABC ve DEF üçgenleri, DE ile BC kenarları birbirine paralel ve bu paralel olan kenarlarının karşısındaki köşeleri ( A ve F köşeleri) diğerinin paralel olan kenarının -şekilde görüldüğü gibi, diğer paralel olan kenar tarafında değil - altıgen oluşturacak biçimde diğer tarafında olmak üzere, AECFBD altıgeninin alanı:
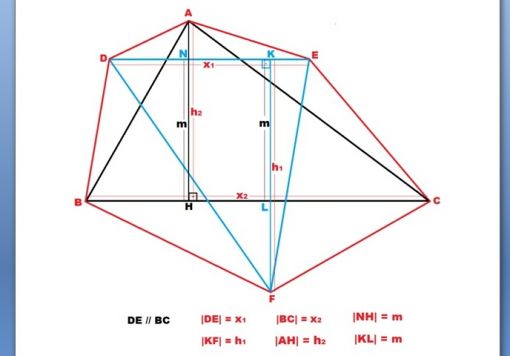
DE // BC olmak üzere,
A (AECFBD) = [ ( X1x h2) / 2 ] + [ (X2 x h1) / 2]
Bu teoremde, iki üçgenin paralel olan kenarlarının eşit olması gerekmez. Eşit olmadığı durumlarda da altıgenin alanı yukarıdaki formül ilebulunabilir. Bu bağıntının en dikkat çekici özelliği,üçgenlerden birinin - diğer üçgeninkine paralel olan- tabanı ile diğer üçgenin yüksekliğinin çaprazlama şekilde çarpılması ve ikiye bölünüp bunların toplanması yoluyla sonuca gidilmesidir.
Kanıt:
AECFBD altıgeninin alanı üç kısma ayrılabilir:
1-ADE üçgeni 2-DECB yamuğu 3- BCF üçgeni
1-ADE üçgeninin alanı:
A(ADE) = [X1 x (h2 – m)] /2
2- DECB yamuğunun alanı:
Yukarıdaki şekilde görüldüğü gibi DECB yamuğunun yüksekliği m uzunluğudur.
A(DECB)= [(X1 + X2)/2] x m
3- BCF üçgeninin alanı:
A (BCF) = [X2 x (h2 – m)] /2
Bu üç alanı bir araya getirdiğimizde,
A (AECFBD) = A (ADE) + A (DECB) + A (BCF)
A (AECFBD) = [X1 x (h2 – m)] /2 + [(X1 + X2) /2] x m + [X2 x (h2 – m)] /2
=[(X1h2– X1m) /2] + [(X1m +X2m) /2] + [(X2h2– X2m) /2]
Bu formüldeki ters işaretli–X1 m ile + X1m ve – X2m ile +X2m birbirini götürdüğü için ifadeyi sadeleştirirsek geriye,
A (AECFBD) = [ (X1 x h2) / 2 ] + [ (X2 x h1) / 2] ifadesi kalır.
Aslında bu formülün paralel olan kenarları eşit uzunlukta olan iki üçgenin köşelerini oluşturduğu altıgen için de geçerli olacağı kolayca fark edilecektir. Formüldeki X1 veX2 uzunlukları eşit olacağı için,yukarıdaki bölümlerde bahsedildiği gibi, iki üçgenin alanlarının toplamı oluştururdukları altıgenin alanına eşit olacaktır.
DOKUZ NOKTA ÇEMBERİNİ OLUŞTURAN NOKTALAR ARASINDA BULUNAN MESAFELERDEKİ EŞİTLİKLER VE BUNLARA BAĞLI SONUÇLAR
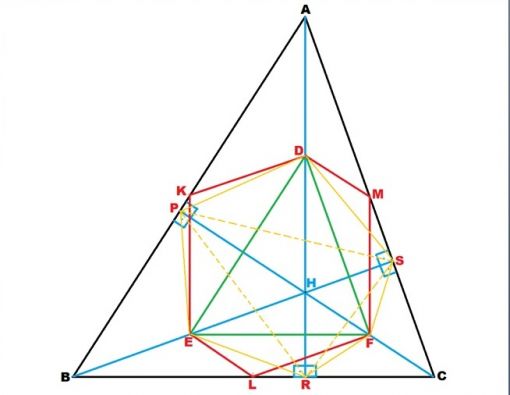
APH dik üçgeninde, D noktası hipotenüsü oluşturan AH nin orta noktası olduğu için, muhteşem üçlü özelliğinden dolayı, P dik köşesinden çıkan PD; AD ve DH’ ye eşittir.
Aynı şekilde, yine muhteşem üçlü özelliğinden AHS dik üçgeni için -burada da D noktası AH’ nın orta noktası olduğundan-DS nin uzunluğu da AD ve DH ye eşittir. Dolayısıyla bunlar yani |PD| ile |DS| birbirine eşit olur.
ABH üçgeninde K noktası AB kenarının orta noktası ve E noktası BH nin orta noktası olduğundan, temel orantı teoremi gereği |KE|, AH kenarının yarısı kadar olan |DH| uzunluğuna eşittir. Dolayısıyla, hemen yukarıda DH’ ye eşit olduğu belirtilen |PD| ve |DS| ile |KE| uzunlukları birbirine eşit olur.
AHC üçgeninde D, AH kenarının ve F noktası ise HC kenarının orta noktası olduğundan, temel orantı teoremi gereği MF, AH’ nin yarısı kadar olan AD ve DH’ ye eşit olur.
|PD| = |KE| = |AD| = |DH| =|DS|= |MF|
ABH üçgeninde K noktası AB kenarının orta noktası ve D noktası AH’nın orta noktası olduğu için, temel orantı teoremi gereği KD’nin uzunluğu BH’nin yarısına eşit olan EH ve BE’ye eşittir. EH ise BPH ve BRH dik üçgenlerindeki muhteşem üçlü özelliklerinden dolayı PE ve ER uzunluklarına eşit olur.
BHC üçgeninde F, HC kenarının orta noktası ve L ise BC nin orta noktası olduğu için temel orantı teoremi gereği LF, BH nin yarısına eşit olan BE ve EH’ ye eşit olacaktır.
|KD| = |EH| = |BE|= |PE| = |ER| = |LF|
BHC üçgeninde E noktası BH kenarının, L noktası ise BC kenarının orta noktası olduğundan, temel orantı teoremi gereği EL, HC kenarının yarısı kadar olan HF ve FC’ ye eşit olur.
HSC ve HRC dik üçgenlerindeki muhteşem üçlü özelliklerinden dolayı, bu iki üçgenin ortak hipotenüsü olan HC nin ortası F noktası olduğu için, SF ve RF birbirine ve aynı zamanda HF ile FC’ ye eşit olur. Biraz yukarıda EL nin HF ve FC ye eşit olduğu belirtildiğinden EL, SF ile RF’ ye de eşit olur.
AHC üçgeninde D, AH nin orta noktası ve M ise AC nin orta noktası olmasından dolayı temel orantı teoremi gereğince DM, HC nin yarısı olan HF ve FC’ ye eşittir.
|EL| = |HF| = |FC| = |SF| = |RF|= |DM|
TEOREM: Yukarıdaki şekilde gösterilen ve yapılan açıklamalardan çıkarılabilecek bir özellik vardır. Şekildeki gibi bir üçgende, yüksekliklerin, diklik merkezinden (H) köşelere kadar olan kısmının orta noktaları ile kenarların orta noktalarının köşelerini oluşturduğu altıgenin (şekildeki DMFLEK altıgeni) alanı, asıl üçgenin alanının (ABC) yarısı (1/2’si) kadardır. Bu özellik yukarıdaki konularda açıklanmıştı. Daha da ilginç olan diğer bir özellik ise şöyledir:
Şekildeki gibi bir üçgende, yüksekliklerin, diklik merkezinden (H) köşelere kadar olan kısmının orta noktaları ile ABC üçgeninin yükseklik ayaklarının (PSR ortik üçgeni) köşelerini oluşturduğu altıgenin (DSFREP altıgeni) alanı da ABC üçgeninin alanının yarısı (1/2’si) kadardır. Yani, DMFLEK altıgeni ile DSFREP altıgeninin alanı birbirine eşittir.
A (DMFLEK) = A (DSFREP) = 1 /2 x A (ABC)
DMFLEK altıgeni ile DMFLEK altıgeninin alanı birbirine eşit olduğunu kanıtı için yukarıdaki şekilde görülen kırmızı ve sarı renkle çizilmiş altıgenlere dikkat çekmek gerekir. Kırmızı renkteki DMFLEK altıgeninin alanı, yüksekliklerin, diklik merkezinden (H) köşelere kadar olan kısımlarının orta noktalarının köşelerini oluşturduğu (yeşil renkli) DEF üçgenine, EKD, DMF ve ELF üçgenlerinin eklenmesiyle bulunur. Eğer, yine DEF üçgenine eklenen EPD, DSF ve ERF üçgenleri EKD, DMF ve ELF üçgenlerinin alanlarına eşit ise DMFLEK ve DSFREP altıgenlerinin alanları da eşit olacaktır. Yukarıdaki eşitliklerden bu konuyu ilgilendirenleri burada tekrar edersek:
|KD| = |PE|, |PD| = |KE|, |DS|= |MF|, |SF| =|DM|, |ER| = |LF|
|EL| = |RF|
|KD| = |PE| ile |PD| = |KE| eşitliği EKD ve EPD üçgenlerinin eşitliğini gösterir. Çünkü her üç kenarı da eşit olan yani eş üçgenlerdir.
Aynı şekilde |DS|= |MF| ile |SF| =|DM| eşitliği DMF ve DSF üçgenlerinin eşitliğini gösterir.
|ER| = |LF| ile |EL| = |RF| eşitliği ise ELF ve ERF üçgenlerinin eşitliğini gösterir.
Dolayısıyla bu bahsedilen üçgenlerin alanları birbirine eşit olduğu için ve bunlar DEF üçgenine eklenerek DMFLEK ve DSFREP altıgenleri oluştuğu için bu altıgenlerin alanları da eşit olur. Aynı zamanda,
A (DMFLEK) = A (DSFREP) = 1 /2 x A (ABC) eşitliklerinin de geçerli olduğunu da hatırlatalım.
TARIK TAŞPINAR (01.08.1972 D.lu)
29 EKİM 2023
CUMHURİYETİMİZİN KURULUŞUNUN 100.YILI VE KURUCUMUZ BÜYÜK ÖNDER MUSTAFA KEMAL ATATÜRK’ÜN ANISINA İTHAFEN…




