matematikkafe.com / Sanat ve Matematik

Müzik, Matematik ve Sonsuzluk

"Müziğin yüksek amacı, kişinin ruhunu İlahi Doğası’na bağlamaktır; eğlenmek değil." Pythagoras

Sadece düşüncede var olan olayların nerelerde uygulama alanı bulabileceği önceden tahmin edilemez. Bu nedenledir ki matematikçiler, yapılan çalışmaları estetik yönden değerlendirmekte, eserlerde bir sanatçı titizliği ile güzellik ve zarafet aramaktadırlar...

Kemanın dizayınında Fibonnaci ve altın oran gözetilir. Serinin ilk 7 sayısına odaklanmak çalgıyı mükemelleştirir.

Orta çağda eğitim programlarında müzik, matematik ve astronomi ile aynı grupta yer alırdı. Matematik ve müzik ilişkisi, günümüzde bilgisayarlar aracılığı ile de devam etmektedir.

Matematiğin müzik üzerindeki etkisini müzik parçalarının yazımında görebiliriz. Belirli bir ritimde, değişik uzunluktaki notalar, belirli bir ölçüye uydurulur. Her ölçünün ise değişik uzunluktaki notaları kullanan belirli sayıda vuruştan oluştuğu görülür.

Pisagor (M.Ö. 580- 500) ve onun düşüncesini taşıyanlar sesin, çekilen telin uzunluğuna bağlı olduğunu fark ederek, müzikte armoni ile tamsayılar arasındaki ilişkiyi kurmuşlardır. Uzunlukları tamsayı oranlarında olan gergin tellerin de armonik sesler verdiği görülmüştür. Örneğin, do sesini çıkaran bir telin uzunluğunun 16/15’i si sesini verirken 6/5’i ise la sesi; 4/3’ü sol sesini; 3/2’si fa sesini; 8/5’i mi sesini; 16/9’u ise re sesini verir.


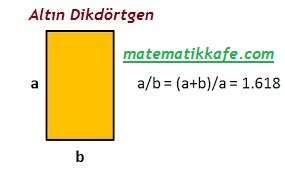
İnsan kulağı için en uyumlu aralığın 8/5 frekans oranındaki major 6’lı olduğu bilinmektedir. Bu oranın altın orana çok yakın bir oran olduğunu görüyoruz.


Görüldüğü gibi iki notayı bir arada duymak, iki frekansı ya da iki sayıyı ve bu iki sayı arasındaki oranı algılamaktan başka bir şey değildir. Demek ki armoni sorunu, iki sayının oranını seçme sorununa eşdeğerdir. Burada müzik, gizli bir aritmetik alıştırmasıdır diyen Leibniz’in haklılığı ortaya çıkıyor.


Müziği, belli kurallara uygun olarak oluşturulmuş basit birtakım seslerin birbirlerini izlemesinden oluşan cümleler topluluğu olarak tanımlayabiliriz. Bu kurallar, matematikte mantık kurallarına karşılık gelirler.

Bir çok müzik aletinin biçiminin matematiksel kavramlarla ilgili olduğunu belirtirsek şaşırmazsınız herhalde. Örneğin, x ≥ 0 için y = 2x eğrisinin grafiği telli ya da üflemeli çalgıların biçimine benzer.


Müzikal seslerin niteliğinin incelenmesi 19. yüzyılda matematikçi J.Fourier tarafından yapılmıştır. Fourier, müzik aleti ve insandan çıkan bütün müzikal seslerin matematiksel ifadelerle tanımlanabileceğini ve bunun da periyodik sinüs fonksiyonları ile olabileceğini ispatlamıştır.


Bir çok müzik aleti yapımcısı, yaptığı aletlerin periyodik ses grafiğini, bu aletler için ideal olan grafikle karşılaştırır. Yine elektronik müzik kayıtları da periyodik grafiklerle yakından ilişkilidir. Görüldüğü gibi bir müzik parçasının üretilmesinde matematikçilerle müzikçilerin birlikteliği çok önemlidir.


"İyi bakıldığı zaman matematik sadece doğruyu değil yüksek bir güzelliği de içerir. Matematik bu güzelliklere bürünmek için insan doğasındaki zayıflıklara başvurmaz; resim ve müziğin göz kamaştırıcı tuzaklarını da kullanmaz." Russel

Kaynak: Prof. Dr. Cihan Orhan

432 Sayısı

432 sayısı, müzikle ilişkili olan frekansın dili hakkında sesin gücünü gösteren kutsal ve derin bir matematik denkleminin parçası. Örneğin pek çok kadim enstrüman, Tibet çanaklarından tutun Kızılderili flütlerine kadar, saniyede 432 tonda titreşen bir tonu üretmektedir. 

Atalarımız bize matematiğin, geometrinin, frekansların ve müziğin derin kodlarına gömülü evrensel bir dil mi bıraktı yoksa?

Janko Piyano Klavyesi

Paul von Jankó tarafından tasarlanan bu alternatif piyano tuş düzeni, piyanistlerin standart bir klavyede çalınması imkansız olabilecek parçaları çalmayı mümkün kılıyor.

Gezegenlerin Müziği

Gezegenlerin ve doğanın da bir müziği vardır. Uzay bir boşluk gibi görülse de bu durum uzayda ses olmadığı anlamına gelmez. Sesler şimdilik bazı araçlarla tespit edilebiliyor. Bu büyüleyici sesler gezegenlerin ve onların halkalarının elektronik titreşimlerinden meydana geliyor...

Evrenin sesini dinlemek için tıklayınız

Müzik ve sonsuzluk ilişkisi, Resim: Monique Dumoulin

 

Hazırlayan: matematikkafe.com

MATEMATİK, MÜZİK VE OYUN!