
ispat-yontemleri
matematikkafe.com
Matematiksel İspat Yöntemleri
"Matematik ispatlar üzerinede yükselir."
"İki tür doğru vardır. Tersinin yanlış olduğu gün gibi ortada olan yüzeysel doğrular ve tersi de doğru olan daha derin doğrular" 
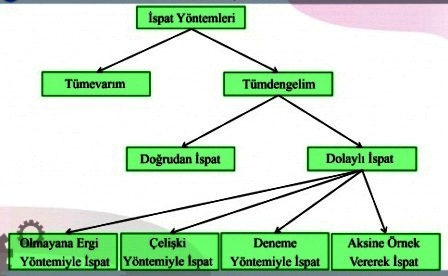
MATEMATİKSEL İSPAT TEKNİKLERİ
1) Doğrudan İspat Yöntemi
Doğru olduğu gösterilmek istenen ifade, doğruluğu kanıtlanmış başka ifadelerle veya aksiyomlarla türetilir.
ÖRNEK
Tüm insanlar ölümlüdür.
Mehmet bir insandır.
Verilen bu iki ifadeyi birleştirerek şu çıkarımı elde ederiz:
Mehmet bir ölümlüdür.
2) Olmayana Ergi Yöntemi
Bu yöntemde doğruluğunu göstermeyi planladığımız ifadenin yanlış olduğunu kabul ederek işe başlıyoruz. Yanlışlığı ispatlama yolunda bir çelişkiye varıyoruz. Sonuç olarak başta yanlış olduğunu kabul ettiğiniz ifadenin aslında doğru bir ifade olduğunu ispatlamış oluyoruz.
Örnek
Sonsuz tane asal sayı vardır.
İspat (Öklid): Varsayalım ki sonlu tane asal sayı olsun:
2,3,5,7,11,.,P
Şimdi bu asal sayıların hepsini çarpıp 1 ekleyelim ve yeni bir sayı tanımlayalım:
K = 2.3.5.7.11.P + 1
Bu sayı tüm asal sayılardan büyüktür, çünkü hepsini birbiriyle çarptık ve bir de ekleme yaptık. Öyleyse K bir asal sayı değildir. Bu durumda K nın kendinden ve 1'den farklı bir asal çarpanı vardır çünkü bileşik (asal olmayan) sayılar asal çarpanlarına ayrılır. Ama K sayısını, hangi asal sayıya bölersek bölelim 1 kalanını elde ederiz ki bu da tam bölünmediğinin yani asal bir çarpanının olmadığının bir göstergesidir. Öyleyse K asal bir sayıdır. Sonuç olarak bir çelişkiye vardık. Yani sonlu tane asal sayı vardır ifadesi yanlıştır. Sonsuz tane asal sayı vardır.
3) Tümevarım Yöntemi
Bu yöntemde ifadenin önce 1 için doğru olduğu gösterilir. Daha sonra n doğal sayısı için doğru olduğu farz edilir ve n+1 doğal sayısı için doğru olduğu gösterilir. Bu da herhangi bir doğal sayı için doğruysa sonraki için de doğru olacağını ispatladığından bütün doğal sayılar için geçerli bir ifade olduğu anlamına gelecektir.
Bu yöntem genelde sonsuz sayıda domino taşlarının dizilmesine benzetilir. n. taşın devrilmesi bir sonraki yani n+1. taşın da devrilmesi anlamına geleceğinden taşların tamamı devrilecektir. Tabi ki yine n=1 için doğruluğunu söylemek lazım. Bunun için de ilk taşı devirmeniz yeterli olacaktır.
MATEMATİK -1 FORMÜLLERİNİN İSPATLARI
Hazırlayan: matematikkafe.com
Yorumlar - Yorum Yaz


